２つの正弦波の位相差を求める方法-04

ベクトル積

2つの正弦波，を以下のように設定しました（振幅で割って，１としています．）

\(\Large x = sin \ ( \omega t) \)　

\(\Large y = sin \ ( \omega t + \phi ) \)　

時間ごとに変化しているので，t = Δt ✕ n，とすると，

\(\Large x_n = sin \ ( \omega \cdot n \Delta t) \)　

\(\Large y_n = sin \ ( \omega \cdot n \Delta t + \phi ) \)　

となります．n+1，ステップでは，

\(\Large x_{n+1} = sin \ \{ \omega \cdot (n+1) \Delta t \} = sin \{ \omega \cdot n \Delta t + \omega \cdot \Delta t\}\)　

\(\Large y_{n+1} = sin \ \{ \omega \cdot (n+1) \Delta t + \phi \} = sin \{ \omega \cdot n \Delta t + \omega \cdot \Delta t + \phi \}\)　

となります．

\(\Large a = \omega \cdot n \Delta t \)

\(\Large b = \omega \cdot n \Delta t + \phi \)

\(\Large c = \omega \cdot \Delta t \)

とすると，

\(\Large x_n = sin \ a \)

\(\Large y_n = sin \ b \)

\(\Large x_{n+1} = sin (a+c) = sin \ a \cdot cos \ c + cos \ a \cdot sin \ c \)

\(\Large y_{n+1} = sin (b+c) = sin \ b \cdot cos \ c + cos \ c \cdot sin \ b \)

これらを二つベクトルと考え，ベクトル積，を考えると，

\(\Large x_{n} \cdot y_{n+1} - x_{n+1} \cdot y_n = sin \ a \cdot (sin \ b \cdot cos \ c + cos \ c \cdot sin \ b) - (sin \ a \cdot cos \ c + cos \ a \cdot sin \ c) \cdot sin \ b \)

\(\Large = sin \ a \cdot sin \ b \cdot cos \ c + sin \ a \cdot cos \ b \cdot sin \ c - sin \ a \cdot sin \ b \cdot cos \ c - cos \ a \cdot sin \ b \cdot sin \ c \)

\(\Large = sin \ a \cdot cos \ b \cdot sin \ c - cos \ a \cdot sin \ b \cdot sin \ c \)

\(\Large = ( sin \ a \cdot cos \ b - cos \ a \cdot sin \ b) \cdot sin \ c \)

\(\Large = sin \ ( a - b ) \cdot sin \ c \)

となります． a, b, c, を戻すと，

\(\Large S = x_{n} \cdot y_{n+1} - x_{n+1} \cdot y_n = sin \ ( a - b ) \cdot sin \ c = sin \ \{\omega \cdot n \Delta t - (\omega \cdot n \Delta t + \phi)\}\cdot sin \ (\omega \cdot \Delta t) \)

\(\Large = sin \ (- \phi) \cdot sin \ (\omega \cdot \Delta t) \)

となります．このことは， 　Sは，ステップによらずに，一定（周波数，位相差，Δｔに依存） ということになります．

このことが何を意味するかというと，

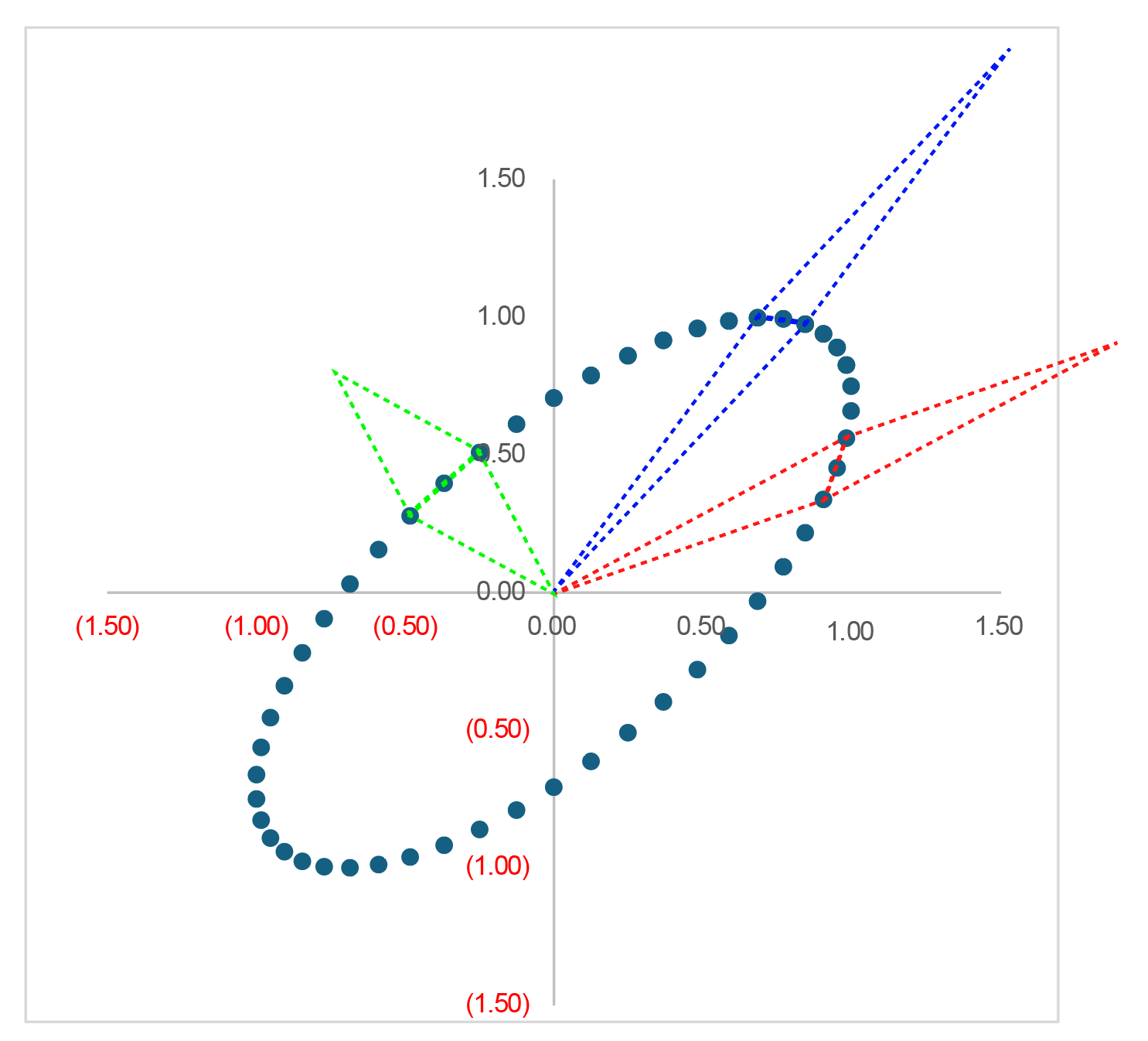
　一定角速度で正弦波運動している２つの波形のXYプロットにおいて，どの軌道位置でも一定間隔の場合のなす平行四辺形（もしくは三角形）の面積は等しい

となります．図示すると，

となり，赤，青，緑で描いた平行四辺形（もしくは三角形）の面積は等しくなります．

位相Φ，角速度ω，Δｔ，のみに依存します．

まるで，ケプラーの第二法則，のようですが，あれは，中心力が働いている場合で，焦点との掃引面積なので，ちょっと違うかもしれません．

Φ=π/2，の場合には円運動になるので，わかりやすいですね．

式をもう一度見直すと，

\(\Large S = x_{n} \cdot y_{n+1} - x_{n+1} \cdot y_n = sin \ (- \phi) \cdot sin \ (\omega \cdot \Delta t) \)

となるので，

\(\Large \phi = - sin^{-1} \left[ \frac{S}{ sin \ (\omega \cdot \Delta t)} \right] = - sin^{-1} \left[ \frac{x_{n} \cdot y_{n+1} - x_{n+1} \cdot y_n}{ sin \ (\omega \cdot \Delta t)} \right]\)

となり，位相情報を，S（たすき掛け），ω，Δｔ，から推定できます．（あらかじめ振幅を，１，としておく必要があります）

元となるサイト，では，
　１．たすき掛け
　２．振幅で割る
　３．相対角周波数で割る
　４．arcsinを計算する
ですが，上記の式はそれをまとめたもの（振幅で割ることは事前に行っている）となります．

次ページに，実際にエクセルで計算した結果をお示しします．